T1 雪花图

题目描述

雪花图是由两个整数 $x$ 和 $y$（均大于 $1$）生成的，生成方式如下：

• 以一个中心顶点开始。
• 将 $x$ 个新顶点与该中心顶点相连。
• 对每一个这 $x$ 个顶点，各自连接 $y$ 个新顶点。

例如，下图是 $x=5$，$y=3$ 的雪花图。

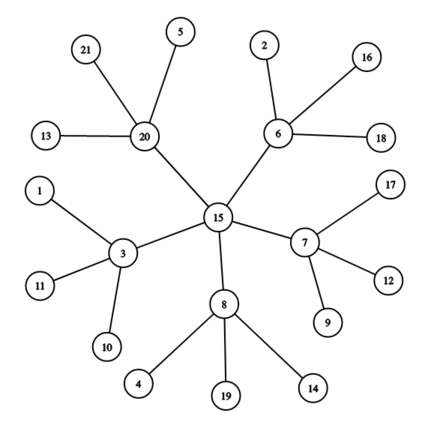
上图中的雪花图有一个中心顶点 $15$，然后有 $x=5$ 个顶点与其相连（$3$、$6$、$7$、$8$ 和 $20$），每个顶点又分别连接 $y=3$ 个顶点。

给定一个雪花图，请你求出 $x$ 和 $y$ 的值。

输入格式

第一行包含一个整数 $t$（$1 \leq t \leq 1000$），表示测试用例的数量。

每个测试用例的第一行包含两个整数 $n$ 和 $m$（$2 \leq n \leq 200$；$1 \leq m \leq \min\left(1000, \frac{n(n-1)}{2}\right)$），分别表示图中的顶点数和边数。

接下来的 $m$ 行，每行包含两个整数 $u$ 和 $v$（$1 \leq u, v \leq n$，$u \neq v$），表示一条连接顶点 $u$ 和 $v$ 的边。图中没有重边和自环。

保证给定的图一定是某组大于 $1$ 的整数 $x$ 和 $y$ 所对应的雪花图。

输出格式

对于每个测试用例，输出一行，包含两个整数 $x$ 和 $y$，用空格分隔，顺序不能颠倒。

输入输出样例 #1

输入 #1

3
21 20
21 20
5 20
13 20
1 3
11 3
10 3
4 8
19 8
14 8
9 7
12 7
17 7
18 6
16 6
2 6
6 15
7 15
8 15
20 15
3 15
7 6
1 2
1 3
2 4
2 5
3 6
3 7
9 8
9 3
3 6
6 2
2 1
5 2
2 7
4 3
3 8

输出 #1

5 3
2 2
2 3

说明/提示

第一个测试用例如题面所示。注意输出 $3\ 5$ 是错误的，因为 $x$ 应该在 $y$ 之前输出。

赛时代码

#include<bits/stdc++.h>
using namespace std;
int t,n,m,cnt[205],mx,ends1[205],u[1005],v[1005];
int check(int x){
	for(int i=1;i<=m;++i){
		if((u[i]==x&&ends1[v[i]]==1)||(v[i]==x&&ends1[u[i]]==1)){
			return 0;
		}
	}
	return 1;
}
int main(){
	cin>>t;
	while(t--){
		int x=0,y=0;
		cin>>n>>m;
		memset(ends1,0,sizeof ends1),memset(cnt,0,sizeof cnt),mx=0;
		for(int i=1;i<=m;++i){
			cin>>u[i]>>v[i];
			cnt[u[i]]++,cnt[v[i]]++;
			mx=max({u[i],v[i],mx});
		}
		for(int i=1;i<=mx;++i){
			if(cnt[i]==1){
				ends1[i]=1;
				y++;
			}
		}
		for(int j=1;j<=n;++j){
			if(ends1[j]!=1&&check(j)){
				x=cnt[j];
			}else if(ends1[j]!=1&&check(j)){
				x=cnt[j];
			}
		}
		cout<<x<<" "<<y/x<<endl;
	}
	return 0;
}

赛后修改

{% notice info %}注意，仅对赛事代码进行精简。{% endnotice %}

#include<bits/stdc++.h>
using namespace std;
int t,n,m,cnt[205],u[1005],v[1005];
int check(int x){
	for(int i=1;i<=m;++i){
		if((u[i]==x&&cnt[v[i]]==1)||(v[i]==x&&cnt[u[i]]==1)){
			return 0;
		}
	}
	return 1;
}
int main(){
	cin>>t;
	while(t--){
		int x=0,y=0;
		cin>>n>>m;
		memset(cnt,0,sizeof cnt);
		for(int i=1;i<=m;++i){
			cin>>u[i]>>v[i];
			cnt[u[i]]++,cnt[v[i]]++;
		}
		for(int i=1;i<=n;++i){
			if(cnt[i]==1)y++;
			if(cnt[i]!=1&&check(i))x=cnt[i];
		}
		cout<<x<<" "<<y/x<<endl;
	}
	return 0;
}

T2 字母对拼接谜题

故事背景

字母王国里流传着一个古老的拼接谜题：传说有一组散落的字母伙伴，每一对伙伴都有着密不可分的羁绊，它们必须紧紧相邻才能发挥魔力。现在，你作为字母王国的解谜者，需要将这些字母伙伴重新组合成一条完整的字母链，让每一对羁绊深厚的字母都能在链中相邻出现。这条字母链的长度恰好比字母对的数量多1，并且如果存在多种组合方式，请给出字典序最小的那一条——这是字母王国传承已久的规则，字典序越小，魔力越纯净。若是无法完成拼接，就只能遗憾地告知王国：无解。

题目描述

给定 n 个各不相同的无序字母对（区分大小写，无序意味着字母对中的两个字母可以交换位置相邻，例如“aZ”与“Za”视为满足相邻要求）。请你构造一个包含 (n+1) 个字母的字符串，使得每个给定的字母对都能在这个字符串中相邻出现。

输入格式

第一行输入一个正整数 n，代表无序字母对的数量。

第二行到第 (n+1) 行，每行输入两个字母，代表一对需要相邻的字母。

输出格式

输出满足要求的字符串。

如果不存在满足要求的字符串，请输出 No Solution。

如果存在多种满足要求的方案，请输出字典序最小的方案（即字符串中前面的字母，其 ASCII 编码尽可能小）。

输入输出样例 #1

输入 #1

4
aZ
tZ
Xt
aX

输出 #1

XaZtX

说明/提示

n 的规模限制如下：

• 25% 的测试数据中，n = 2
• 50% 的测试数据中，n ≤ 10
• 75% 的测试数据中，n ≤ 100
• 100% 的测试数据中，n ≤ 600

T3 广义斐波那契图

题目描述

给定一个包含 $n$ 个顶点和 $m$ 条边的有向图。每个顶点 $v$ 上对应一个正整数 $a_v$。请你统计所有由至少两个顶点组成的不同简单路径，使得沿路径经过顶点的数字序列构成一个广义斐波那契数列。

在本题中，若数列 $x_0, x_1, \ldots, x_k$ 满足以下条件，则称其为广义斐波那契数列：

• $x_0, x_1$ 为任意自然数。
• 对所有 $2 \le i \le k$，都有 $x_i = x_{i-2} + x_{i-1}$。

注意，广义斐波那契数列至少包含两个数字。

由于答案可能很大，输出其对 $998\,244\,353$ 取模的结果。

一个简单路径指在有向图中按顺序经过顶点 $v_1, v_2, \ldots, v_k$，且所有顶点至多出现一次，并且对于所有 $i < k$，存在从 $v_i$ 到 $v_{i+1}$ 的有向边。

输入格式

每个测试点包含若干组测试数据。第一行为测试数据组数 $t$（$1 \le t \le 10^4$）。每组测试数据包括：

第一行，两个整数 $n$ 和 $m$（$2 \le n \le 2 \cdot 10^5$，$1 \le m \le 2 \cdot 10^5$）——图中顶点数和边数。

第二行为 $n$ 个正整数 $a_1, a_2, \ldots, a_n$（$1 \le a_i \le 10^{18}$）——每个顶点上的数字。

接下来 $m$ 行，每行两个正整数 $v, u$（$1 \le v, u \le n$，$u \ne v$），表示一条从 $v$ 到 $u$ 的有向边。保证不存在重边。

保证所有测试数据中 $n$ 的总和与 $m$ 的总和不超过 $2 \times 10^5$。

输出格式

对于每组测试数据，输出广义斐波那契路径的数量，对 $998\,244\,353$ 取模。

输入输出样例 #1

输入 #1

4
4 4
3 4 3 6
1 2
1 3
2 4
3 4
4 6
1 1 1 2
1 2
2 3
3 1
1 4
2 4
3 4
8 11
2 4 2 6 8 10 18 26
1 2
2 3
3 1
4 3
2 4
3 5
5 6
4 6
6 7
7 5
5 8
2 2
10 10
1 2
2 1

输出 #1

5
9
24
2

说明/提示

第一个样例的解释（顶点编号在括号外，顶点上的数字在括号内）：

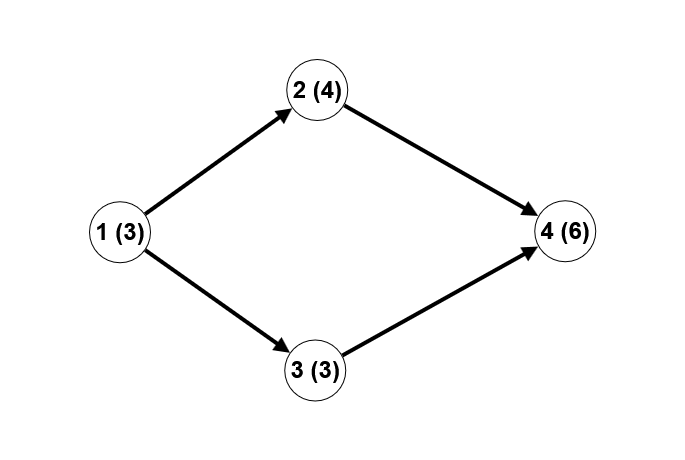
本例中共有 5 条广义斐波那契路径：(1, 2), (1, 3), (2, 4), (3, 4), (1, 3, 4)。例如，路径 (1, 3, 4) 沿途顶点上的数字序列为：[3, 3, 6]，可以看到第三个数字等于前两个数字之和。

第二个样例的解释：

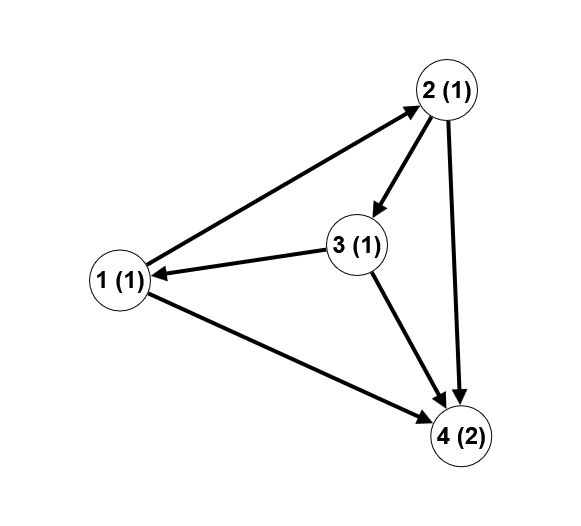
本例中共有 9 条广义斐波那契路径：(1, 2), (1, 4), (2, 3), (2, 4), (3, 1), (3, 4), (1, 2, 4), (2, 3, 4), (3, 1, 4)。注意，路径 (1, 2, 3) 上的数字序列为：[1, 1, 1]，这不是广义斐波那契数列。